An oscillator is the basic element of ac signal sources and generates sinusoidal signals of known frequency and amplitude.
The main applications of oscillators are as sinusoidal waveform sources in electronic measurements. Oscillators can generate a wide range of frequencies (from a few Hz to many GHz) as per the application’s requirement. Even though, an oscillator can be considered as generating sinusoidal signal, it merely acts as energy converter, converting a dc source of supply to alternating current of desired frequency.
An oscillator is generally an amplifier with positive feedback. An oscillator has a gain equal to or slightly greater than unity. In the feedback path of the oscillator, capacitor, inductor or both are used as reactive components. In addition to these reactive components, an operational amplifier or bipolar transistor is used as amplifying device. No external ac input is needed to cause the oscillator to work as the dc supply energy is converted by the oscillator into ac energy.
Feedback circuit used in oscillators
It is the use of positive feedback that results in a feedback amplifier having closed-loop gain Af greater than unity and satisfies the phase condition.
In a system assuming, Vin, and Vout as the input and output voltages respectively.
Without feedback or open gain loop gain, then

Taking the forward path gain of the system as A and β as feedback factor; with feedback, the output voltage of the system:
Recommended: The Ultimate Guide to Electrical Maintenance


Where Af is the closed loop gain
Oscillators generate a continuous voltage output waveform at a required frequency with the values of the inductors, capacitors, or resistors forming a frequency selective LC resonant (tank) feedback network. The oscillator frequency is usually regulated using a tuned or resonant inductive/capacitive circuit with the resulting output frequency termed to as the oscillation frequency. For that reason, the feedback of the oscillator is made reactive. The phase angle of the feedback will vary as a function of frequency and this is called phase shift. Certain conditions must be met for sustained oscillations, and they include:
- The loop gain of the circuit must be equal to or greater than unity
- The phase shift of the circuit must be zero
These 2 conditions for sustained oscillations are termed to as Barkhausen Criteria.
Resonance
If a constant voltage with varying frequency is impressed to a circuit consisting of an inductor, capacitor and resistor, then the reactance of both the capacitor-resistor (RC) and inductor-resistor (RL) paths are to change both in amplitude and in phase of the output signal as compared to the input signal. At high frequencies the reactance of a capacitor is very low and it acts as a short circuit while the reactance of the inductor is high and acts as an open circuit. At low frequencies, the opposite is true, meaning the reactance of the capacitor acts as open circuit, and the reactance of the inductor as a short circuit.
Between these two boundaries, the combination of the inductor and capacitor produces a tuned or resonant circuit that has a resonant frequency (fr) in which the capacitive and inductive reactances are equal and cancel out each other, leaving only the resistance of the circuit to oppose the flow of the current and as a result of that, there is no phase shift as the current is in phase with voltage.
Don’t miss out on key updates, join our newsletter List
The operation of a basic LC oscillatory circuit

The circuit consists of an inductive coil L and a capacitor C. The capacitor stores energy in the form of an electrostatic field and which produces a potential or static voltage across it, while the inductive coil stores its energy in the form of a magnetic field.
The capacitor is charged up to the dc supply voltage V by putting the switch in the position A. When the capacitor is fully charged, the switch is thrown to the position B and the charged capacitor is now connected in parallel across the inductive coil, so the capacitor begins to discharge itself through the coil. The voltage across C starts falling as the current through the coil begins to rise. The rising current sets up an electromagnetic field around the coil and when C is completely discharged, the energy that was originally stored in the capacitor C as an electrostatic field is now stored in the inductive coil L as an electromagnetic field around the coil windings.
As there is no external voltage in the circuit to maintain the current within the coil, it starts to fall as the electromagnetic field begins to collapse. A back emf is induced in the coil i.e.

This back emf keeps the current flowing in the original direction. This current now charges the capacitor C with opposite polarity to its original charge. C continues to charge until the current has fallen to zero and the electromagnetic field of the coil has collapsed completely. The energy originally introduced into the circuit through the switch has been returned to the capacitor which again has an electrostatic potential across it, but now of opposite polarity. The capacitor now starts to discharge again back through the coil and the whole process is repeated; with polarities changed and continues as the energy is passed back and forth producing ac type sinusoidal voltage and current waveform.
This oscillatory action of transferring energy from the capacitor C to the inductor L and vice versa would continue indefinitely if there is was no loss of energy in the circuit. But energy is lost, in the resistance of the inductor coil, in the dielectric of the capacitor, and radiation from the circuit, so the oscillation steadily decreases until it does away completely. In a practical LC circuit, the amplitude of the oscillatory voltage decreases at each half cycle of oscillation and will eventually die away to zero. When this happens, the oscillations are said to be damped. The quality factor of the circuit sets the amount of damping.
The frequency of the oscillatory voltage depends upon the value of the inductance and capacitance in the LC circuit. We know that for resonance to occur both capacitive Xc and inductive XL reactances must be equal and opposite to cancel out each other. As a result, the resistance in the circuit remains to oppose the flow of current. The frequency at which this happens is given as follows:

To maintain the oscillations, keeping the amplitude at a constant level, in an LC circuit, it is required to replace the energy lost in each oscillation. The amount of energy replaced must equal to that lost during each cycle. Otherwise, if the amount of energy replaced is too small the amplitude would decrease to zero overtime. The simplest way of replacing this energy is to take part of the output from the LC circuit, amplify it and then feed it back into the LC circuit gain. This can be achieved by using a voltage amplifier. To produce a constant oscillation, the level of the energy fed back to the LC network must be accurately controlled. To maintain a stable oscillation the overall gain of the circuit must be equal to 1 or unity. Any less and the oscillations will not start or die away to zero, any more, the oscillations will occur but the amplitude will become clipped by the supply rails causing distortions.
Related: The Fundamentals of Oscillators in Communication Systems
How a BJT is used as a LC oscillator amplifier
A bipolar Junction Transistor (BJT) is used as the oscillator amplifier and the tuned LC circuit acts as the collector load as shown in the circuit below:
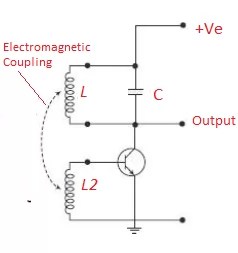
A second coil L2 is connected between the base and emitter. Electromagnetic field of L2 is mutually coupled with that of the coil L. Mutual inductance exists between the two circuits. The changing current in one circuit, induces by electromagnetic induction a potential in the other due to the transformer action. So as the oscillations take place in the tuned circuit, electromagnetic energy is transferred from the coil L to the coil L2 and a voltage of the same frequency as that in the tuned circuit is applied between the base and emitter of the transmitter. In this way, the necessary automatic feedback is obtained. The amount of feedback can be varied by changing the coupling between L and L2. When the circuit is oscillating, its impedance is resistive and the collector and base voltages are 180° out of phase. In order to maintain oscillations, the voltage applied to the tuned circuit must be in phase with the oscillations occurring in the tuned circuit, so it is necessary to introduce an additional 180° phase shift into the feedback path between the collector and base. This is done by winding the coil of L2 in the correct direction relative to the coil L giving us the correct amplitude and phase relationships for the oscillator circuit or by introducing a phase shift between the output and input of the amplifier.
LC oscillators are essentially sinusoidal oscillators or harmonic oscillators that can generate high-frequency sine waves for use in Radio Frequency (RF) applications with the transistor amplifier being a BJT or FET. These harmonic oscillators come in different forms and the common types are listed below.
Common Types of LC Oscillators
- Hartley oscillator
- Colpitts oscillator
- Wien bridge oscillator
- Crystal oscillator
- RC oscillator
Also read: Basic Features of Crystal Oscillators

Leave a Reply
You must be logged in to post a comment.